ACL 2018
Sentiment Analysis를 위한 Domain adaptation
Introduction
본 논문에서는, word embedding을 domain-sensitive, sentiment-aware하게 학습시키고, words의 domain 파악과 함께 sentiment analysis를 목적으로 한다.
Related Work
결국에는 18년도 ACL에 쏟아져 나온 논문들과 함께 domain 관련 문제점을 해결하려는 시도다. word embedding이 target domain에서 (혹은 general domain에서) 학습되었을 경우 단어의 의미가 domain-dependent하여 sentiment analysis가 원활하지 못하다. 많은 단어들이 domain에 따라 단어의 opinion이 바뀌는 경우가 많기 때문이다. 예를 들어 unpredictable은 movie domain에서는 positive지만 automobile domain에서는 negative다.
이전의 시도들에서는 domain 간 common feature를 찾아 이용했었지만 본 논문에서는 domain-common & domain-specific embedding을 모두 사용한다.
본 논문과 같이 multiple domain을 고려한 word embedding을 학습하는 논문들도 있는데, 대부분은 여러 domain에서 분리된 embedding을 학습시킨다. 그 이후 frequency-based statistical measure로 pivot words를 골라서 각 embedding space를 연결해 준다. 본 논문에서는 domain-common words는 sentiment information과 context words를 이용하여 결정된다.
Model, DSE
DSE (Domain-sensitive and Sentiment-aware word Embeddings) 라고 부른단다.
multiple domain 환경에서 가능한데 논문에서는 일단 2개의 domain 위에서 설명하였고 그 이상의 경우에서 어떻게 적용하는지 소개해 놓았다.
Design of Embeddings
각 word \(w\)에 대해 latent variable \(z_w\)를 부여, \({z_w}=1\)이면 \(w\)는 common, 아니면 \(w\)는 domain p나 q에 specific.
원하는 모델을 얻기 위해 word2vec에 변형을 시키는데 먼저 skip-gram의 단어 \(w\)일 때 주변 단어 \(w_t\)의 확률 식이 아래와 같다.
\[p({w_t}|w)=\sum_{k \in \{0,1\}} p({w_t}|w, {z_w}=k)p({z_w}=k)\]원래는 \(z_w\) 관련 항 없이 \(w\)에 대한 \(w_t\)가 되어야 하는데 \(z_w\) dependent하게 만들었다.
그렇다면 \(z_w=1\), 즉 \(w\)가 domain-common word일 경우, 아래와 같은 식을 얻을 수 있다.
\[p({w_t}|w, z_w=1)= \frac{exp(U_w^c \cdot V_{w_t})}{\sum_{w^ \prime \in \Lambda} exp(U_w^c \cdot V_{w^ \prime })}\]요렇게 된다. 여기서 중요한 건 \(U_w^c\)가 바로 word2vec에서 word vector로 쓰이는 부분과 같은 역할을 하는 것. word \(w\)가 domain-common일 때의 word embedding이 된다.
\(z_w=0\), 즉 \(w\)가 domain-specific word일 경우, 아래와 같은 식을 얻을 수 있다.
\[p({w_t}|w, z_w=0)= \begin{cases} \frac{exp(U_w^p \cdot V_{w_t})}{\sum_{w^ \prime \in \Lambda} exp(U_w^p \cdot V_{w^ \prime })}, & \text{if $w \in D^p$} \\ \frac{exp(U_w^q \cdot V_{w_t})}{\sum_{w^ \prime \in \Lambda} exp(U_w^q \cdot V_{w^ \prime })}, & \text{if $w \in D^q$} \end{cases}\]여기서 \(D^p\)와 \(D^q\)는 각각 p 도메인과 q 도메인을 말한다. \(U_w^p\)는 p 도메인에 대하여 domain-specific인 \(w\)의 word vector가 된다.
Exploiting Sentiment Information
앞까지는 word vector의 확률 분포를 정의한 것이었다. 근데 그 식들이 사용되려면 \(z_w\), 즉 domain-commonality가 필요하다.
아직 단어의 polarity (positive or negative) 를 안 써줬다. 걔네까지 이용해서 모델을 만들고 EM method로 \(z_w\)를 구한다. 먼저 polarity \(y_w\)를 도입하면,
\[p({y_w}|w)=\sum_{k \in \{0,1\}} p({y_w}|w, z_w=k)p(z_w=k)\]\(z_w=1\)일 경우 \(w\)는 domain-common word이고,
\[p(y_w=1|w, z_w=1)=\sigma (U_w^c \cdot s)\]여기서 \(\sigma (\cdot)\)은 sigmoid 함수를 의미한다. \(s\)는 \(d\)차원을 가진 sentiment-boundary vector.
\[p(y_w=0|w, z_w=1)=1-p(y_w=1|w, z_w=1)\]만약 \(w\)가 domain-specific word일 경우,
\[p(y_w=1|w, z_w=0)= \begin{cases} \sigma (U_w^p \cdot s), & \text{if $w \in D^p$} \\ \sigma (U_w^q \cdot s), & \text{if $w \in D^q$} \end{cases}\]Inference Algorithm
domain \(D^p, D^q\)는 주어진 것으로 한다. 그리고 EM 알고리즘을 사용하는데…….

논문 한 페이지를 꽉 채우는 식들을 다 봐야한다. 논문을 직접 보는 것을 추천…
참고로 domain이 3개 이상일 경우 \(z_w\)의 확률분포를 Bernoulli에서 Multinomial로 바꾸면 된다.
Experiment
Amazon 제품 리뷰 데이터에서 제품 카테고리 별로 나눈 걸로 여러 도메인 데이터가 있다고 친다. books(B), DVDs(D), electronics(E), kitchen appliances(K), 총 4가지 데이터셋을 이용한다.
text와 1-to-5 score가 있는데, 3 이상은 positive, 미만은 negative review로 본다.
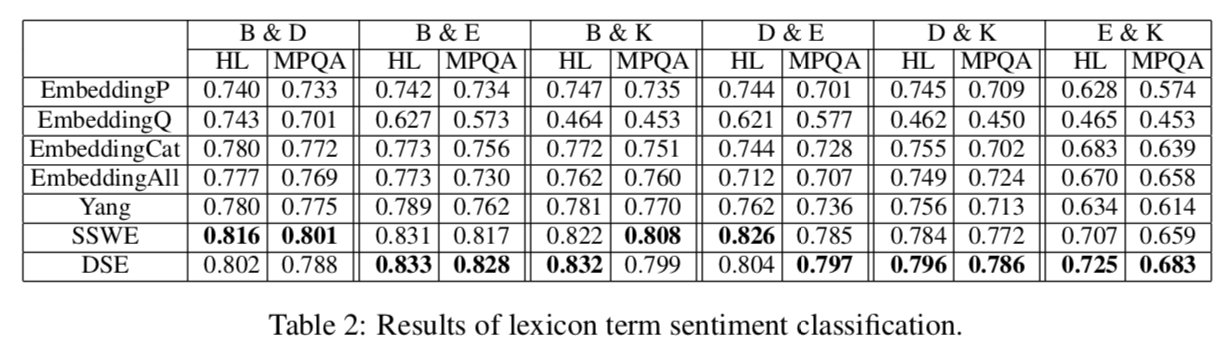
Results